The Logarithmic Spiral

"Although changed, I rise again the same." -Jacques Bernoulli, Spira Mirabilis

Mathematical Properties of the Spiral

As we saw here, a logarithmic spiral is a fascinating by-product of self-similar geometric constructions. The spiral possesses several mathematically-interesting properties, each of which is outlined in detail in Mukhopadhyay. We will consider each briefly. But first, some necessary background:

The polar equation of a logarithmic spiral is written as r=e^(a*theta), where r is the distance from the origin, e is Euler's number (about 1.618282), and theta is the angle traveled measured in radians (1 radian is approximately 57 degrees)
The constant a is the rate of increase of the spiral. The sign of a determines the direction of rotation of the spiral (see below).

A left-handed logarithmic spiral generated by a>0, image from Mukhopadhyay 39

A right-handed logarithmic spiral generated by a<0, image from Mukhopadhyay 40

Now on to the mathematical properties. Only two of the several noted by Mukhopadhyay will be noted here:

r increases proportionally and remains in proportion with the golden ratio as theta increases if we define the equation as above, multiplied by e^(a*phi). The reasons for this are more thoroughly discussed by Mukhopadhyay.
Any line segment drawn through the origin always intersects a logarithmic spiral at a constant angle.

The Spiral in Nature

We have seen how the logarithmic spiral is related to the golden ratio, and now we shall see its prevalence in nature and natural forms, from microscopic unicellular organisms to enormous galaxies containing hundreds of billions of stars. We will work our way up in size, starting with the smallest instance and moving to the largest.

Unicellular foraminifera showing a logarithmic spiral pattern, image from http://tinyurl.com/2382ldf

M-74 Gemini Spiral Galaxy, image from http://tinyurl.com/3ykkp2p

The most popular appearance of a logarithmic spiral is in the shell of the chambered nautilus. As the mollusk within grows, it builds larger and larger chambers in its shell, and seals off the smaller ones that are left unused. The shell's overall shape remains unchanged as the creature grows. Similar spirals are found in rams' horns and elephant tusks (Livio "Story," 117).

The shell of a chambered nautilus, image from http://tinyurl.com/2aoj4od

A ram's horn in the shape of a (non-coplanar) logarithmic spiral, image from http://tinyurl.com/275tnff

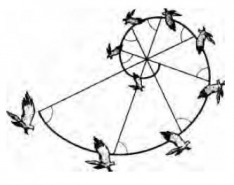
The logarithmic spiral also appears in the flight patterns of peregrine falcons, most likely due to the second property discussed above (that the spiral is equiangular). The spiral allows the birds to keep their heads straight when flying (because their eyes are on either side of their head, they need to cock their heads 40 degrees to take full advantage of their sight range). The spiral pattern allows them to maintain maximal speeds while eliminating drag from a cocked head (Livio, "Story," 120).

Peregrine falcon flight patterns along an equiangular spiral, image from Livio 119.

As noted above, spiral galaxies also adopt a logarithmic shape. This is because they consist of a relatively thin disk of gas, dust, and stars all rotating around the center. The closer an object (or set of objects, like our solar system) is to the galactic center, the faster it moves, and so a spiral is formed. Classical physics, however, tells us that under these conditions the galaxy should eventually wind in on itself, but this is not observed. Scientists have explained this using the concept of "density waves" of gas compression that squeeze gas clouds and trigger new star formation. Thus, the spirals we observe from earth are simply markers of the denser-than-average parts of the galaxy. These waves are the result of a gravitational force originating in the fact that the galaxy lacks a perfectly-symmetric distribution of matter (Livio "Story" 121-122).

(a) A set of oval orbits around a center; (b) the same orbits slightly perturbed. Image from Livio 122.

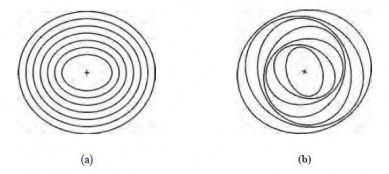
In the image above, we see that if each oval orbit in (a) is rotated slightly in a manner that changes with distance from the center results in a spiral pattern. This is a direct consequence of Newton's Law of Universal Gravitation (Livio "Story," 122).