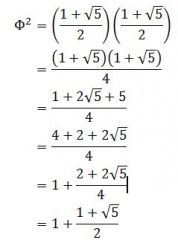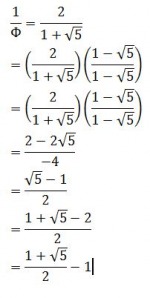Mathematical Properties of Phi

The Golden Ratio is very interesting in mathematics for multiple reasons, first and foremost because its square and reciprocal have some rather peculiar properties (Tung 7). Note that when we square phi (that is, multiply it by itself), we see that the result is equal to phi plus one: 

Derivation of Phi Squared

Also, the reciprocal of phi (1/phi) is equal to phi minus one:

Derivation of Reciprocal Phi

Both of these properties can be deduced from the various definitions of phi found here.