Geometric Constructions Involving Phi

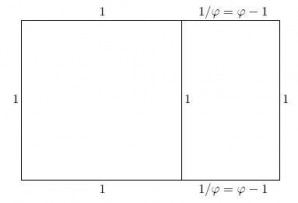
One may hear much talk about so-called "golden shapes," mainly the rectangle. Simply put, a golden rectangle is one whose sides exhibit the golden ratio: the length of the rectangle divided by the width is either phi or 1 minus phi, which, as seen here, is equivalent to 1 divided by phi.

A golden rectangle, image from http://tinyurl.com/y7vcpa9

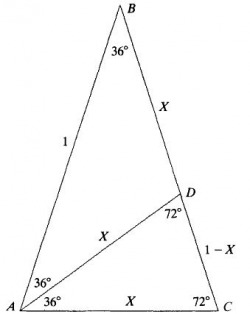
Another common figure is the golden triangle, in which the ratio of a side to the base is phi.

A golden triangle, image from Markowski 3

Notice that in the above figure, angle A has been bisected to create two additional, self-similar triangles (i.e., the measures of their internal angles and the ratios between the sides are identical no matter the length of the sides). This process can be repeated indefinitely and is used to generate pentagons, pentagrams, and decagons of various size.


Self-similarity is also a property of golden rectangles. By removing a square of side length equal to the length of the short side of the rectangle, one can create another golden rectangle.

A partitioned golden rectangle, image from http://tinyurl.com/y7vcpa9

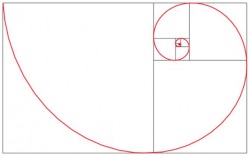
If this partitioning process continues (using either a rectangle or a triangle), a spiral is generated:

A golden spiral generated from a golden rectangle, image from http://mathworld.wolfram.com/GoldenRectangle.html

A golden spiral generated from a golden triangle, image from http://tinyurl.com/y7plynh

These spirals are called logarithmic spirals, named for the way the radius of the spiral grows when moving around it in a clockwise direction. These spirals have fascinated scientists and mathematicians for quite some time, as they abound in nature and can be seen in things from small chambered nautiluses to galaxies of incomprehensible size. (Livio, "Story" 119). Logarithmic spirals will be discussed in more detail here.

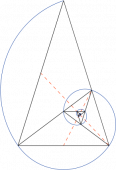
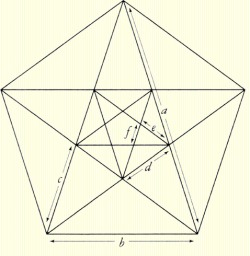
We can also see the golden ratio at work in another construction involving pentagons (five-sided polygons) and pentagrams (five-pointed stars).

Self-similarity in five-sided figures, image from http://tinyurl.com/3yurfwk

Each of the "measured" triangles above is a golden triangle (see above), and therefore has the property that the ratio of the larger side to the smaller side (i.e., the ratio of a to b in the figure above) is exactly the golden ratio. This astounded the ancient Pythagoreans and led to the discovery of incommensurability in numbers. See here for more information.