Architectural and Aesthetic Approximations
"The measurement of architecture is always problematic because, as architecture can never provide an 'exact' Golden Mean, any argument must be derived from approximate conclusions." -Michael J. Ostwald, Under Siege: The Golden Mean in Architecture
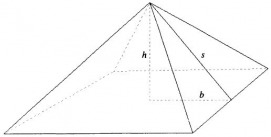
We first consider the myth that the Great Pyramid was "designed so that the ratio of the slant height of the pyramid to half the length of the base would be phi" (Markowski 6). The height of the Pyramid is given as 481.4 feet and the average length of the sides of the base is 755.79 feet. Using the Pythagorean Theorem, we see that the ratio of the slant height to half the sides of the base is about 1.62, which is only 0.1% different from phi. However, in examining this claim, Markowski notes that the claim seems to originate with writings by the ancient Greek historian Herodotus, who supposedly wrote that the Pyramid's dimensions were chosen so the area of a square of length equal to the height equaled the area of a face triangle, thus implying that the ratio of slant height to half the base is exactly phi (Proof!). Yet, a literal translation of the original Greek shows that Herodotus did not make that claim (Markowski 7). Also, Herodotus wrote roughly two millennia after the Pyramid was built, so his insight into the minds of the original builders must be questioned. Also, the ancient Egyptians had no concept of irrational numbers, and so could not have centered the design around phi (Dudley).
Another hugely popular claim about phi in architecture is that it can be seen to be embodied in the Parthenon. "To support this claim authors often include a figure...where the large rectangle enclosing the end view of the Parthenon-like temple is a golden rectangle. None of these authors is bothered by the fact that parts of the Parthenon are outside the golden rectangle" (Markowski 8). For example, in the image below (click to enlarge), notice that the outer rectangle encloses slightly more than just the structure itself, particularly on the bottom.
Accurate measurements of the Parthenon are actually quite variable, due to both variation among authors and imprecise construction (Markowski 8-9; Stecchini). Markowski mentions two different measurements of the Parthenon, both of which fall outside of what is known in statistics as the "critical region," which allows for 5% variation in a sample proportion either above or below the true value. It is thus highly unlikely that the Parthenon's architecture displays phi-like properties.
This imprecise measurement has also been applied to various works of art, specifically Leonardo Da Vinci's Mona Lisa. Theorists claim that if one draws a rectangle around the face of the famous subject, the ratio of the height to the width of that rectangle is equal to the Golden Ratio. However, "no documentation exists to indicate that Leonardo consiously used the Golden ratio in the Mona Lisa's composition, nor to where precisely the rectangle should be drawn" (Livio, "Aesthetics").
Note that in the above image of the Mona Lisa the rectangle is drawn in starting at the hairline rather than the top of the head, and the ratio of the lengths of the sides is roughly 14:9, or 1.5556, which falls outside the 5% critical region for phi. If the rectangle were to extend to the top of the head, the ratio would be about 16:9, or 1.7778, which also falls outside the critical region. However, surrealist Salvador Dali did include elements of the Golden Ratio in his painting entitled Sacrament of the Last Supper. The painting itself is very close to being in the shape of a golden rectangle (my imprecise, unscientific calculations showed a ratio of about 1.6396, which does fall within 5% of the true value of phi. Also, the painting contains a dodecahedron, in which both the surface area and the volume are functions of phi (for dodecahedrons of side length 1) (Livio, "Aesthetics").