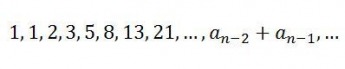The Fibonacci Sequence
As mentioned before, the Golden Ratio shows up all over the place in mathematics, usually in mathematical modeling involving the Fibonacci sequence (Tung 7). Its prevalence is mainly due to the fact that the golden ratio is derived from geometry. Each term in the Fibonacci sequence is the sum of the two terms previous to it. Thus, the sequence progresses:
It can be shown by rigorous proof of calculus that the limit of the n-even terms (the second, fourth, sixth... terms in the series) and the limit of the n-odd terms (first, third, fifth...) as n gets extremely large (i.e., as the number of terms approaches infinity) are identical. Furthermore, they must satisfy the equation (x^2)-x-1=0 and are therefore the golden ratio.
Properties of the Fibonacci Numbers
The Fibonacci numbers have a few rather interesting properties that are of note:
- The product of any four consecutive Fibonacci numbers is the area of a Pythagorean triangle.
- The Fibonacci numbers are complete, that is, every positive integer can be written as a sum of individual terms in the sequence. Interestingly, if one term is removed from the sequence it is still complete, but removing two terms makes it incomplete.
- The ratio of alternating Fibonacci numbers (i.e. 1, 2, 5, 13, ...) converge to one over phi squared.