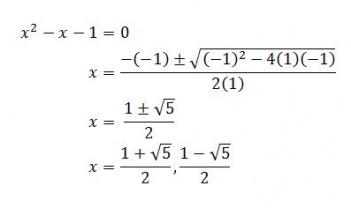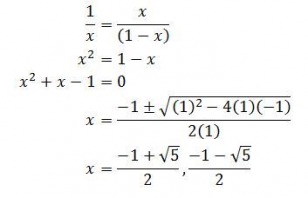The Mathematical Definitions of Phi
Let's start with a working definition of our number. Phi is defined as the positive, irrational solution to the quadratic equation x^2-x-1=0. If we apply the Quadratic Formula to solve this, we get:
Let's start with a working definition of our number. Phi is defined as the positive, irrational solution to the quadratic equation x^2-x-1=0. If we apply the Quadratic Formula to solve this, we get:
Remember, we're only interested in the POSITIVE solution ((1+sqrt(5))/2). The negative solution is not nearly as interesting as our friend phi.
Another definition of phi involves what Euclid (an ancient Greek mathematician and the father of modern geometry) called "division in extreme and mean ratio," which divided a line segment at such a point so that the ratio of the whole segment to the larger piece is equal to the ratio of the larger piece to the smaller piece (Markowski 2). It's helpful to use a picture here:
Another definition of phi involves what Euclid (an ancient Greek mathematician and the father of modern geometry) called "division in extreme and mean ratio," which divided a line segment at such a point so that the ratio of the whole segment to the larger piece is equal to the ratio of the larger piece to the smaller piece (Markowski 2). It's helpful to use a picture here:
So here we have a line segment of length 1 and we consider the ratios 1/x and x/(1-x). Then we have:
Note that the negative solution is negative phi, and the positive solution is actually 1/phi. These numbers have rather special mathematical properties, which will be discussed here.
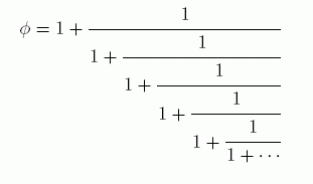
There is one final way to define phi, and it takes the form of a continued fraction extended infinitely:
There is one final way to define phi, and it takes the form of a continued fraction extended infinitely:
This last method has lead to mathematicians referring to phi as the most irrational number. Because this continued fraction is composed entirely of ones, it converges extremely slowly. "The Golden Ratio is, in this sense, more 'difficult' to express as a fraction than any other irrational number--it is the 'most irrational' among irrationals" (Livio "Story" 85).